What time were you leaving ?
Probably around 2ish. I will text you the location
 Feel free to hang out and lurk as long as you like. However, we would like to encourage you to register so that you can join the community and use the numerous features on the site. After registering, don't forget to post up an introduction!
Feel free to hang out and lurk as long as you like. However, we would like to encourage you to register so that you can join the community and use the numerous features on the site. After registering, don't forget to post up an introduction!
What time were you leaving ?
That looks like a good evening. Little jealous.
Did you bring that tree with you?


Actually not far from what he does sometimes IIRC.Maybe put the hammock over the campfire. He would be smoked and ready to eat by morning.
Hey Mister... have you been to this one? Looks like theres even old logs in the outlying area if a person had an axe. Could even check on the state boundary markers just to the west
Thompson Grove Campground
(575) 374-9652

Wow, 7 hours! Maybe not.
Shared route
From Colleyville to Thompson Grove Campground via US-287 N.
7 hr (457 mi)
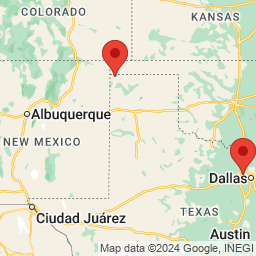
Colleyville to Thompson Grove Campground
maps.app.goo.gl
I think some of the state parks would be fun to camp at.
I am glad to see you guys got some time to spend with each other.
Did anyone ask about the bug splatters on your ski suit?
You must have been really hauling *** down that mountain!
I still have and wear my Klim suit on just about every ride! It saved my hide in Utah and will be there if I ever need it again. I bought the wife the same suit last year.
Sent from my iPhone using Tapatalk
Trips planned for this year:
May NM BDR - Cloudcroft to Antonio CO. Will probably use the CDR tracks.
June: Nelson BC.
Leave June 19thAM from Amarillo return Amarillo on July 1. Airbnb at Amarillo the 18th and 1st.
Hang out for a few days in Nelson BC (Koutenay Bay Area). There are several motorcycle Campgrounds in the area. Base camp and spend a few days riding dirt roads.
There will be 4 x400 mile days to get there and 4 x400 mile days back. I will spend 4 nights at Toad Rock. I will be camping at campgrounds up and back.

Toad Rock Home
Where the sound of bikes, is the sound of friends. Where the sound of bikes, is the sound of friends. Welcome to Toad Rock! Situated on 34-forested acres, Toad Rock is located on Kootenay Lake in the West Kootenay region of British Columbia... the landwww.toadrockcampground.com
July: Wyoming and Florida with Sharon
August: S.Dakota and Gila TWT rally in NM
September: MABDR
October: probably Arkansas
November or December: big bend either before Thanksgiving or after Christmas.
The NM BDR we can accommodate 1 more riders, the Ma Bdr is full
Looking for 2 or 3 ADV riders for British Colombia. This trip will have a Super laid back vibe.


